При изучении математики ученики начинаются знакомиться с различными видами геометрических фигур. Сегодня речь пойдет о различных видах треугольников.

Определение

Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.

Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.

Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.

Рис. 1. Треугольник ABC.

Виды треугольников

Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.

Существует три вида треугольников по углам:

• остроугольные;
• прямоугольные;
• тупоугольные.

Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .

Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.

Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.

Рис. 2. Виды треугольников по углам.

Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.

Причем, большая сторона является гипотенузой.

Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.

Виды треугольников по сторонам:

• равносторонние;
• равнобедренные;
• разносторонние.

Равносторонний треугольник – это треугольник, у которого все стороны равны. Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.

Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.

Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.

Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.

Рис. 3. Виды треугольников по сторонам.

Сумма всех углов треугольника, независимо от его вида, равна 1800.

Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.

Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.

Задача:

Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?

Решение:

Для решения данного задания нужно использовать неравенство a

Что мы узнали?

Из данного материала из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.

Треугольником называют фигуру, состоящую из трех соединенных между собой точек. В зависимости от углов треугольник может быть:

• Прямоугольным , если один из углов равен 90 градусов;
• Тупоугольный , если один из углов тупой, т.е. больше 90 градусов;
• Остроугольным , если все углы треугольника острые.

Для решения задач с остроугольными треугольниками часто приходится использовать теорему синусов или косинусов.

Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.

Характеристики

В остроугольном треугольнике каждый угол меньше 90 градусов. Но сумма углов в треугольнике всегда равна 180. В любой фигуре вершины обозначают заглавными латинскими буквами.

Одним из элементов треугольника, вместе со сторонами и углами, является внешний угол. Внешний угол это угол, смежный с внутренним углом треугольника.

У любого треугольника 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым.

Линии остроугольного треугольника

Остроугольный треугольник обладает рядом свойств.

Медиана будет равняться половине длины той стороны геометрической фигуры, на которую она опущена. Причем можно провести этот отрезок с любой вершины.

Рис. 1. Медианы в остроугольном треугольнике

Известно, что если провести три высоты в остроугольном треугольнике, то они будут пересекаться в одной точке, которую называют ортоцентром. Эти отрезки опускают под прямым углом к противоположным сторонам. Высоты в остроугольном треугольнике разделяют эту фигуру на подобные треугольники.

Рис. 2. Высоты в остроугольном треугольнике

Биссектрисы в остроугольном треугольнике не только делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.

Также биссектриса разделяет сторону остроугольного треугольника на две части, которые пропорциональны соответствующим сторонам. Данное утверждение нужно запомнить, чтобы решать некоторые задачи.

Рис. 3. Биссектрисы в остроугольном треугольнике

Свойства

Если суммировать числовые значения любых двух сторон остроугольного треугольника, то обязательно получим цифру, которая будет больше третьего отрезка данной геометрической фигуры.

Средняя линия в остроугольном треугольнике параллельна одной из сторон данной фигуры и равняется половине ее половине.

Что мы узнали?

В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равняется 180 градусов. Нельзя забывать о характерных линиях треугольника. Поскольку с их помощью легко вычислить стороны данной треугольной фигуры или центр определенной окружности. А если в условиях задач по геометрии указаны углы, то можно воспользоваться тригонометрическими функциями.

Тест по теме

Оценка статьи

Средняя оценка: 4.5 . Всего получено оценок: 114.

Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.

Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.

Сумма углов треугольника.

Внешний угол треугольника. Признаки равенства треугольников.

Замечательные линии и точки в треугольнике: высоты, медианы,

биссектрисы,срединны e перпендикуляры, ортоцентр,

центр тяжести, центр описанного круга, центр вписанного круга.

Теорема Пифагора. Соотношение сторон в произвольномтреугольнике.

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые (рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21), то это прямоугольный треугольник ; стороны a , b , образующие прямой угол, называются катетами ; сторона c , противоположная прямому углу, называется гипотенузой . Если один из углов тупой ( B, рис.22), то это тупоугольный треугольник.


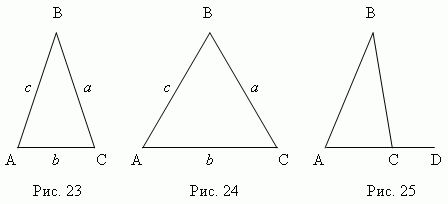
Треугольник ABC (рис.23) - равнобедренный , если две его стороны равны (a = c ); эти равные стороны называются боковыми , третья сторона называется основанием треугольника. Треугольник ABC (рис.24) – равносторонний , если все его стороны равны (a = b = c ). В общем случае (a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний

угол BCD. Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B.

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности (a < b + c , a > b – c ;b < a + c , b > a – c ;c < a + b ,c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (точка O , рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (точка O , рис.27) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

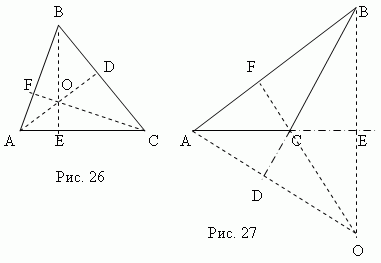
Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника (AD , BE , CF , рис.28) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника (AD , BE , CF , рис.29) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

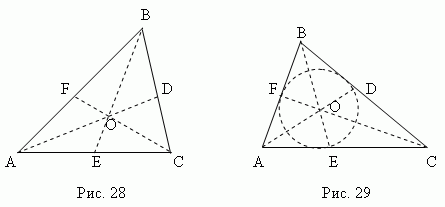
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС (KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга (точки K , M , N – середины сторон треугольника ABC ).

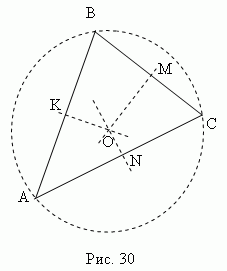
В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

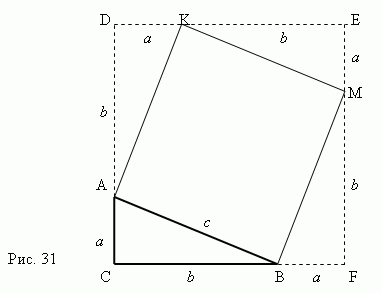
Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна (a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

c 2 + 4 (ab / 2) = c 2 + 2 ab ,

отсюда ,

c 2 + 2 ab = (a + b ) 2 ,

и окончательно имеем:

c 2 = a 2 + b 2 .

Соотношение сторон в произвольном треугольнике.

В общем случае (для произвольного треугольника) имеем:

c 2 = a 2 + b 2 – 2ab · cos C,

где C – угол между сторонами a и b .

Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.

Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).

Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 - четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника , отрезки - его сторонами . Стороны треугольника образуют в вершинах треугольника три угла.

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).

Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

Рис. 6. Тупоугольный треугольник

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).

Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми , третья сторона - основанием . В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Рассмотрите рисунки.

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились с различными видами треугольников.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. - М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. - М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. - М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. - М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. - М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. - М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. - М.: «Экзамен», 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются … , отрезки - его … . Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.

Некоторый треугольник , в котором все стороны не одинаковой длины, принято называть разносторонними .

Треугольник, с двумя одинаковыми сторонами обозначают как равнобедренный . Одинаковые стороны принято именовать боковыми , третью сторону - основанием. В равной мере будет верным и такое определение основания треугольника - это сторона равнобедренного треугольника, которая не равна двум другим сторонам.

В равнобедренном треугольнике углы при основании равновелики. Высота , медиана , биссектриса равнобедренного треугольника, прочерченные к его основанию, совмещаются.

Треугольник , со всеми одинаковыми сторонами, обозначают как равносторонние или правильные . В равностороннем треугольнике все углы по 60°, а центры вписанной и описанной окружности совмещены.

Типы треугольников в зависимости от параметров углов.

Треугольник , в котором только углы меньше 90 0 (острые), именуют остроугольным .

Треугольник, в котором представлен угол 90 0 , именуют прямоугольным . Стороны треугольника, формирующие прямой угол, принято обозначать катетами , а сторона расположенная напротив прямого угла - гипотенузой .